Einstein was wrong. Speed of Gravity is faster than light.

Abstract

 In this abstract, we explore the properties of matter and energy and how much they can be compressed. We can understand that the radius of matter in its minimum state is about almost half of the Schwarzschild radius. When we calculate the escape velocity at this radius, we get a constant value V_e = 4.24 \times 10^8m/ s for any given mass. The Escape velocity at Schwarzschild radius is equal to the speed of light. Using this value we can conclude that the speed of gravity is faster than light. It is clear that the Schwarzschild radius is not the actual radius of the mass. The Schwarzschild radius is the distance from the center of a mass to the point in space-time where even light cannot escape from it. So, the matter can shrink further than the Schwarzschild radius.

Introduction

This idea mainly evolves from my published article “The Structure of the Relatively Accelerating Universe”.  This will provide a significant boost to our efforts in space exploration. This will enable us to significantly increase the speed of spaceships even further. The General Theory of Relativity explains how an object is precisely situated in space-time. This concept extends it further. At the core of this concept is how an object utilizes space-time. The interaction between matter and space-time forms the foundation of our universe. That phenomenon is what we know as gravity. That’s why Einstein regarded space-time as a dimension. All matter always carries with it a corresponding amount of space-time, proportional to its mass. This is the insight I gained from a thorough observation of the universe. It has the potential to alter our current conception of the universe. For that, we must comprehend the dimensions of both space-time and matter.

Concept

Here, I am using Planck units to develop the idea. I consider a unit Planck mass (m_{\rho}) as a system. The key idea of this concept is that the unit Planck mass perfectly fits into the Planck volume, leaving no free space inside this system. Therefore, the radius of this system will always be equal to the Planck length (l_{\rho}). Let us examine how this system relates to its space-time. According to this concept we can say that m_{\rho}=l^3_{\rho}. If the mass m_{\rho}=l^3_{\rho}, then the quantised value of length l_{\rho} concerning m_{\rho} will be as follows: l_{\rho} = \sqrt[3]{m_{\rho}}. 

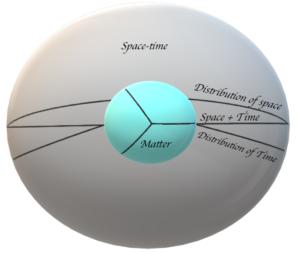
Figure 1 : Structure of maximum compressed mass with associated Space-time

In the figure, the inner sphere represents the amount of matter contained in a system. The outer sphere represents the space-time that the mass inside can influence. Here, matter possesses three dimensions (length, width, and depth), as well as mass. These three dimensions also apply to space-time. There, space and time interact with each other according to the amount of matter contained in that system. At the outermost part of the image, you can see that the amount of space that mass can influence is zero. But there, time is at its highest strength. It is the endpoint of space-time under the influence of matter within that system. Here, time can reach its maximum velocity. It can be observed that the strength of time decreases and the strength of space increases as we approach the matter that is part of the system. This phenomenon is a result of the increasing influence of matter on space. Decrement in the strength of time and increment in the strength of space occur in the same proportion. So, the strength of time and space are equal inside the system. Since the strength of space is highest at the surface of matter within the system, the strength of time becomes zero. So the quantised values (strength) of length (space) and time are equal. So the quantised value of Planck time also equal to \sqrt[3]{m_{\rho}} . If we consider matter alone, we can see that it also has three dimensions, just like space. However, time has no significance in that context. It will contain only matter. Nothing can enter or travel within it. Time is meaningless where it cannot be traversed.

A similar situation occurs in a black hole. Inside a black hole, matter shrinks to its minimum volume. Let’s examine what happens when an atom is absorbed by a black hole. Inside the nucleus of an atom, there is a lot of space between the protons and neutrons. There is even more space available between the nucleus and the electrons. When an atom is absorbed into a black hole, its constituent particles are compressed to their smallest possible state within the black hole. The space inside the atom is absorbed into space-time of the black hole. Here, a distinction is made between matter and space-time. 

Now, we can try to find out the actual radius of a black hole when it shrinks to its minimum volume. So, we can use the formula \frac{4}{3}\pi r^3 to find the volume of a sphere here. But we know that objects have different masses. Adding each unit of Planck mass will correspondingly add a proportional amount of space-time to the system. To elucidate the nature of larger objects, their mass must be compared to the Planck mass. Therefore, it is necessary to understand the quantity of Planck mass contained within the object. We can quickly comprehend it by using this equation.

m_{A\rho} = \frac{m}{m_{\rho}}

Here m_{A\rho} represents the ratio of Planck mass within the object, m represents the actual mass of the object, and {m_{\rho}} represents the Planck mass. m_{A\rho} is variable according to the mass of the object. We can further extend equation (1) to describe objects containing more than one Planck mass and find the volume of the object.

V_T = \frac{4}{3}\pi (m_{A\rho}l_{\rho})^3

Here, l_{\rho} represents the Planck length and  m_{A\rho}l_{\rho} is the radius of that object. This is because adding each unit of Planck mass to a system increases its corresponding Planck length. We already know the Schwarzschild radius \frac{2Gm}{r^2}. This radius m_{A\rho}l_{\rho} will be the actual radius of any mass if it shrinks to its minimum. So, with this equation, we can find the actual radius of any mass. For example, if we calculate the Schwarzschild radius of the Planck mass, it would be 3.22724978 \times 10^{- 35} meters. It is roughly twice the Planck length 1.616 \times 10^{- 35} m. So it has already been proved in quantum mechanics that the actual radius of any mass is not equal to the Schwarzschild radius. More information regarding this is recorded in Table 1. 

Object	Mass	Ratio in Planck mass	Minimum Radius	Escape Velocity at minimum radius	Schwarzschild radius	Escape Velocity at Schwarzschild radius
Planck mass	2.176 \times 10^{- 8}kg	1	1.616 \times 10^{- 35}m	4.24 \times 10^8m/ s	3.22724978 \times 10^{- 35}m	3 \times 10^8m/ s
Electron	9.1093837 \times 10^{- 31}kg	4.185 \times 10^{23}	6.672 \times 10^{- 58}m	4.24 \times 10^8m/ s	1.35102282 \times 10^{- 57}m	3 \times 10^8m/ s
Sun	1.989 \times 10^{30}kg	9.14 \times 10^{37}	1.477024 \times 10^3m	4.24 \times 10^8m/ s	2.949928 \times 10^{- 3}m	3 \times 10^8m/ s
Earth	5.97 \times 10^{24}kg	2.74356618 \times 10^{32}	4.43360294 \times 10^{- 3}m	4.24 \times 10^8m/ s	8.854 \times 10^{- 3}m	3 \times 10^8m/ s

You can watch the detailed video presentation here.

In this table we can see the minimum radius and Schwarzschild radius of Planck mass, Electron, Sun, and Earth. We can find the minimum radius is approximately half of the Schwarzschild radius. It is clear that the Schwarzschild radius is not the actual radius of the mass. The Schwarzschild radius is the distance from the center of a mass to the point in space-time where even light cannot escape from it. We know the equation for Schwarzschild radius r_{Sc} = \frac{2Gm}{c^2}. It depends upon Universal gravitational constant, mass of the object, and speed of light. So it can be said that the Schwarzschild radius is the minimum radius to which a mass must be compressed for it to become a black hole. If the mass is contained within this radius, the escape velocity at the surface would be equal to the speed of light, meaning not even light can escape the gravitational pull. So at this point the speed of gravity and the speed of light are equal. So, if the mass can shrink more, the gravitational force will increase. The speed of light cannot increase because it is constant. We can clearly say that the mass can shrink more than the limit of Schwarzschild radius. Because the Schwarzschild radius is almost double of Planck length. Anyhow, here we have found the equation to calculate the minimum radius which a mass can ever achieve. So if we calculate the escape velocity with the minimum radius of a mass we will get a constant value V_{eMinimumradius} = \frac{2Gm}{c^2}. So with the result we can say that the speed of gravity is faster than light. And the maximum speed which gravity can achieve is 4.24 \times 10^8m/ s.  

Now, we can scale and describe the entire universe in one dimension. I have described the dimensional arrangements within a system in my book ‘Key to the Secrets of the Universe’. Now let’s apply this concept to the equation e = mc^2, focusing solely on mass and volume. Here, we can start again with a unit of Planck energy e_{\rho} = m_{\rho}(\frac{l_{\rho}}{t_{\rho}})^2. Let’s examine how it can transition into either a particle or a grandiose structure. This equation describes a system comprising both matter and space-time. Matter can exert an effect on space-time proportional to its mass. Just as we know that energy cannot be created or destroyed, space-time also cannot be created or destroyed. I have already stated that c^2 or (\frac{l_{\rho}}{t_{\rho}})^2 represents the amount of space-time that a unit Planck mass  can influence. We have already derived the quantized values of Planck length and Planck time in this theory. Indeed, applying the quantized values of Planck length and Planck time to the equation e = mc^2 will lead us to intriguing insights and revelations. 

e = m(\frac{\sqrt[3]{m_{\rho}}}{\sqrt[3]{m_{\rho}}})^2

It can be understood that the quantized value of space-time (\frac{\sqrt[3]{m_{\rho}}}{\sqrt[3]{m_{\rho}}})^2 is 1, which indicates a fundamental and indivisible aspect of the universe. We can understand that the distribution of energy in space-time is uniform everywhere. That is, space-time under the influence of mass is uniformly distributed everywhere. Let us imagine any point in space-time as an example. Where the distribution of space is more, the distribution of time is less. The distribution of time is proportional to the distribution of space. If we add the strength of space with the strength of time at any point of space-time, it will always be a constant value. This implies that the effect of energy on space-time is uniform throughout the universe. This concept is the only way to reach Quantum gravity. That is why our universe exists, based on the influence of gravity. Gravitation would not be possible if the influence of energy of two different objects on their respective space-times were different. The biggest example of this is our solar system. If the Sun’s influence on its own space-time and the Earth’s influence on its own space-time were in different proportions, the Earth would not be able to exist within the Sun’s space-time.

We have already discussed how the strengths of space and time work inside space-time with Figure 1.  Therefore, at any point the distribution of space-time will be the same. So, the graviton, the particle responsible for gravitational interaction, can maintain its mass precisely anywhere in space-time. Upon reaching the surface of the outer sphere, the distribution of space becomes 0, and the distribution of time becomes its maximum. This does not mean that space-time or gravity ends here, because the distribution of space-time is still the same. Because time here holds the force of space-time and continues to do so. It’s just that the influence of that particular mass on space-time from that point is zero in the three spatial dimensions (length, width, and height). The space-time of any mass is always bound to the space-time of the universe. We can understand that the dimension of time plays an important role in connecting 2 different space-times. The proof of this is that the strength of space in outer space is very weak. As an extension of this idea I have already calculated the estimated radius of space-time of each of the above objects. But this time I am unable to present it here. Because while I am calculating the escape velocity, there seems to be some mismatch. I hope I can clear it as soon as possible.

This situation can describe the entire universe. We can use the same situation to explain the behavior of an atom or a star. Then we must also consider the space inside the atom or star as part of the space-time of the system. When we look at the volume of space inside an atom or star, the beginning of their space-time is near their center.

Here, matter and space-time are part of one system, but they are two separate entities that can never merge into one. To test this, let’s examine how space-time functions in two distinct scenarios. Let’s first closely observe the planetary motion of Earth around the Sun. Earth lies within the gravitational field of the Sun, which is a curvature in space-time caused by the Sun’s mass. So, indeed, Earth exists within the space-time framework influenced by the Sun’s gravity. Similarly, Earth also creates its own gravitational field, which is a curvature in space-time with similar characteristics to that of the Sun. The position of the Moon is within Earth’s space-time. That is why the moon can move along with the earth. That is, along with Earth, its space-time also orbits the Sun. Similarly, the Moon also has a similar space-time. Here we can observe three different space-times, each of them moving along with the masses that influence them. Now let’s consider another scenario for examination. Imagine that you are throwing a stone into an ocean. Here the Stone is Sinking into the water by leaving its space-time to the Earth’s space-time. Archimedes’ principle provides evidence supporting this situation. If space-time of the stone were to immerse in water along with it, there would be a separation between the water and the stone. However, in reality, this separation does not occur. Here, the stone contributes its space-time to that of the water as it sinks into it. If we take the stone out of the water, it can return to its original space-time state. Matter merges with matter, and space-time merges with space-time.

Exactly, this concept is analogous to what occurs in phenomena like the photoelectric effect and black holes, where the interaction between particles or massive objects leads to the exchange or merging of space-time properties. In the photoelectric effect, when an electron absorbs a photon, its space-time is added to the electron’s space-time. Similar phenomena occur in black holes. Now we can understand, with examples, that matter can utilize its space-time in two ways. A photon traveling through space-time can also interact with space-time in this manner. A photon can travel while retaining its space-time properties, or it can move freely by merging its space-time with the space-time through which it travels. We need to delve into a more detailed understanding of space-time.

Conclusion 

In summary, the concept of space-time provides a unified framework for understanding the interconnected nature of space and time. Matter influences space-time, and in turn, space-time influences the behavior of matter. Through examples like planetary motion, the photoelectric effect, and black holes, we observe how matter and energy interact with space-time, exchanging properties and shaping the dynamics of the universe. This holistic perspective challenges traditional notions of space and time as separate entities, emphasizing their inseparable relationship within the fabric of reality. As we continue to explore and unravel the mysteries of space-time, we gain deeper insights into the fundamental nature of the cosmos and our place within it. A better understanding of the distribution of space and time in space-time will indeed facilitate our space journeys, enabling more precise navigation, planning, and optimization of space missions.

Acknowledgment:

I want to express my sincere gratitude to the pioneers in theoretical physics, whose groundbreaking work has paved the way for our understanding of the fundamental nature of space and time. Additionally, I acknowledge the invaluable support and encouragement provided by Mrs. Takashima Hiromi throughout this journey of exploration and discovery. Finally, I thank the readers and researchers who engage with this theory, as their curiosity and insights continue to drive progress and innovation in our understanding of the universe.

References

1. Aloysius Sebastian: Structure of Relatively Accelerating Universe DOI: 10.4236/ijaa.2014.41015
2. Aloysius sebastian: Key To The Secrets Of Universe: Explore The Universe https://www.amazon.com/dp/B0B9M4CNLB
3. “The Mathematical Principles of Natural Philosophy”, Encyclopædia Britannica, London, archived from the original on 2 May 2015, retrieved 13 February 2015
4. How can we become superhuman??: Evolution to the superhuman and prison-less community of the type 1 civilization. https://www.amazon.com/dp/B0C9Y194L7
5. Planck, Max (1899). “Über irreversible Strahlungsvorgänge”. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin (in German). 5: 440–480. Archived from the original on 17 November 2020. Retrieved 23 May 2020. pp. 478–80 contain the first appearance of the Planck base units, and of the Planck constant, which Planck denoted by b. a and f in this paper correspond to the k and G in this article.
6. Einstein A. (1916), Relativity: The Special and General Theory  (Translation 1920), New York: H. Holt and Company
7. Einstein, Albert (28 November 1919). “Time, Space, and Gravitation” . The Times.
8. Aloysius Sebastian: Key to the secrets of the universe ASIN: B0C9S4VGTZ https://www.amazon.com/dp/B0B9M4CNLB
9. Gorelik, Gennady (1992). “First Steps of Quantum Gravity and the Planck Values”. In Eisenstaedt, Jean; Kox, Anne J. (eds.). Studies in the History of General Relativity: Based on the proceedings of the 2nd International Conference on the History of General Relativity, Luminy, France, 1988. Boston: Birkhäuser. pp. 364–379. ISBN 0-8176-3479-7. OCLC 24011430. Archived from the original on 25 April 2019.
10. Penrose, Roger (2005). The Road to Reality. New York: Alfred A. Knopf. ISBN 978-0-679-45443-4.
11. Bose, Mainak Kumar (1988). Late classical India. A. Mukherjee & Co. Archived from the original on 13 August 2021. Retrieved 28 July 2021.
12. Feynman, R.P.; Morinigo, F.B.; Wagner, W.G.; Hatfield, B. (1995). Feynman lectures on gravitation. Addison-Wesley. ISBN 978-0-201-62734-3.
13. Sen, Amartya (2005). The Argumentative Indian. Allen Lane. p. 29. ISBN 978-0-7139-9687-6.
14. Bose, S.; et al. (2017). “Spin Entanglement Witness for Quantum Gravity”. Physical Review Letters. 119 (4): 240401. arXiv:1707.06050. Bibcode:2017PhRvL.119x0401B. doi:10.1103/PhysRevLett.119.240401. PMID 29286711. S2CID 2684909.
15. Stephani, Hans (2003). Exact Solutions to Einstein’s Field Equations. Cambridge University Press. p. 1. ISBN 978-0-521-46136-8.
16. Hawking, Stephen W. (1987). “Quantum cosmology”. In Hawking, Stephen W.; Israel, Werner (eds.). 300 Years of Gravitation. Cambridge University Press. pp. 631–651. ISBN 978-0-521-37976-2.
17. Bose, Sougato; Mazumdar, Anupam; Morley, Gavin W.; Ulbricht, Hendrik; Toroš, Marko; Paternostro, Mauro; Geraci, Andrew A.; Barker, Peter F.; Kim, M. S.; Milburn, Gerard (2017-12-13). “Spin Entanglement Witness for Quantum Gravity”. Physical Review Letters. 119 (24): 240401. arXiv:1707.06050. Bibcode:2017PhRvL.119x0401B. doi:10.1103/PhysRevLett.119.240401. PMID 29286711. S2CID 2684909. Archived from the original on 2023-01-22. Retrieved 2022-07-13.
18. Barvinsky, A. O.; Vilkovisky, G. A. (1990). “Covariant perturbation theory. 2: Second order in the curvature. General algorithms”. Nuclear Physics B. 333: 471–511. doi:10.1016/0550-3213(90)90047-H.
19. Marletto, C.; Vedral, V. (2017). “Gravitationally Induced Entanglement between Two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity”. Physical Review Letters. 119 (24): 240402. arXiv:1707.06036. Bibcode:2017PhRvL.119x0402M. doi:10.1103/PhysRevLett.119.240402. PMID 29286752. S2CID 5163793.
20. Pickover, Clifford (16 April 2008). Archimedes to Hawking: Laws of Science and the Great Minds Behind Them. Oxford University Press. ISBN 9780199792689. Archived from the original on 18 January 2017. Retrieved 29 August 2017.
21. Thomson, J. J. (1897). “XL. Cathode Rays”. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 44 (269): 293–316. doi:10.1080/14786449708621070. ISSN 1941-5982.Schrödinger, E. (1926). “An Undulatory Theory of the Mechanics of Atoms and Molecules”. Physical Review. 28 (6): 1049–1070. Bibcode:1926PhRv…28.1049S. doi:10.1103/PhysRev.28.1049. ISSN 0031-899X.
22. Darrigol, O. (2005), “The Genesis of the theory of relativity” (PDF), Séminaire Poincaré, 1: 1–22, Bibcode:2006eins.book….1D, doi:10.1007/3-7643-7436-5_1, ISBN 978-3-7643-7435-8, archived
23. Poincare, Henri (1906). “On the Dynamics of the Electron (Sur la dynamique de l’électron)”. Rendiconti del Circolo Matematico di Palermo. 21: 129–176. Bibcode:1906RCMP…21..129P. doi:10.1007/bf03013466. hdl:2027/uiug.30112063899089. S2CID 120211823. Archived from the original on 11 July 2017. Retrieved 15 July 2017.
24. “The Fate of the First Black Hole”. www.science.org. Retrieved 30 May 2022.
25. “Gravity Probe B: FAQ”. Archived from the original on 2 June 2018. Retrieved 2 July 2017.
26. Overbye, Dennis (8 June 2015). “Black Hole Hunters”. NASA. Archived from the original on 9 June 2015. Retrieved 8 June 2015.
27. Savitt, Steven. “Being and Becoming in Modern Physics. 3. The Special Theory of Relativity”. The Stanford Encyclopedia of Philosophy.
28. Mould, Richard A. (1994). Basic Relativity (1st ed.). Springer. p. 42. ISBN 978-0-387-95210-9. Retrieved 22 April 2017.
29. Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics (2nd ed.). W. H. Freeman. ISBN 0-7167-2327-1.
30. Tangherlini, F. R. (1963). “Schwarzschild field in n dimensions and the dimensionality of space problem”. Nuovo Cimento. 27 (3): 636–651. Bibcode:1963NCim…27..636T. doi:10.1007/BF02784569. S2CID 119683293.