Quantum gravity
The theory of the Universe presents a unified framework that intertwines the dimensions of space and time, providing a deeper understanding of the fundamental fabric of the universe. In this abstract, we explore the concept of space-time and its implications on the behavior of matter and energy. We can explain the entire universe with one equation. Basic dimensions such as mass, time, and length can be unified and measured on a single scale, providing a comprehensive understanding of the fundamental properties of the universe. This unification allows us to gain deeper insights into the properties of the graviton, the interacting particle of gravitational force, and accurately calculate its mass. It is evident that matter can utilize space-time in two distinct manners, enabling an object to traverse through space-time via two distinct modes of interaction.
We are discussing gravity and we are going to unify all the dimensions. This is a theory that explains the basic nature of energy at the Planck scale. These are the smallest dimensions we know of. By starting from the very smallest possible units, we can realize the fundamental nature of energy. Here I am considering Planck volume as the smallest space, which a unit of Planck energy can accommodate perfectly. Let us consider this as a closed system. This system will not allow any space inside it. As we have seen in the Big Bang Singularity. A system that is completely filled with energy. So here we can consider Planck energy and Planck volume as the same, with different units. With this concept, we can relate the fundamental units of mass, time, and length with the dimensional units of length, breadth, and height. Here we imagine that there is only one such system in the universe. We need to get acquainted with a single-window system, to understand more about gravity. For the time being, we can assume that there is no other system that exists in the universe, to exert gravitational influence on this. So what we are going to discuss here, is the gravity of this system. At this stage, we can see that gravity is the result of the work done by unit Planck energy in a unit Planck volume. The result of this work allows the system to spread its influence into space-time, which will create a curvature in space-time. This theory allows an object to maintain different strengths, in its gravitational fields, at different distances. It asserts that a gravitational system can have only a limited range. At a certain level, the distribution of its gravitational field will be zero. The curved space-time of a gravitational system has a fixed volume. If the system increases its volume, it will decrease the strength of the gravitational field. The system expands its volume means that space is allowed within it. Starting from the very smallest units, this theory allows us to explain the nature of larger masses, by adding energy in a system on the Planck scale. Starting from very small units, by adding new energy to a system on the Planck scale, this theory allows us to explain the behavior of large masses. By considering mass as just a dimension of energy, it says mass is one of the reasons for gravity. This theory allows the quantization of length and time inside the Planck volume. So the total energy of the system will determine the gravity of a system. The volume of a system is not interfering directly with gravity, but its Planck scale volume will determine the gravity of this system. By quantizing time and length, this theory suggests the possibility of changing the dimensional arrangements of the system. Different dimensional configurations of a system will allow the system to show different properties. The character of a system will be determined by its dimensional configurations. So a system can change dimensional configurations related to the situations. This concept will allow the energy to be self-consistent and conscious inside the Planck volume. Energy itself acts as the source of life. So the probability of the existence of life on any part of our universe is very high.
As we know, matter (Energy) can exist in different sizes. Energy is familiar to us as large forms, such as the sun and stars, and smaller forms, such as atoms and particles. Here I am trying to know more about the properties of the extremely smallest possible forms of energy. In physics, we are using the Planck units to represent the smallest measurements. So, I am also starting with the Planck units. We can now say that Planck Energy is the smallest form of energy present in the universe. Similarly, in particle physics, we can see that particles exhibit different properties such as spin, charge, and many others. I am that much curious, to know about the reasons for all these properties. Here I would like to summarize the facts, which I have realized from such thoughts, about the physical world surrounding me. It is an introduction, to my understanding of my surroundings. In physics, we are dividing the concepts about our universe into two different fields, microscopic and macroscopic and both of them are explaining to us the incredible nature of our universe. The more we know about the universe, the more we can see new questions arise. This is just the beginning of my journey, to discover the secrets that the universe hides in its beauty.
All these things are well described in my book. You can buy the book here.

The General Theory of Relativity is the best, to understand the visible universe. And it is explaining to us, the mysterious phenomenon which we call gravity, at its best. Albert Einstein presented his theory with all its charms. He revealed to us a series of realities that were never met with common sense, and which would change all our imaginations. Still, we are on the search for a theory of gravity, of the microscopic universe, which can describe the entire properties of energy and by the whole universe, by itself. Thus, our knowledge of the phenomenon of gravity is incomplete. Einstein’s theory deals with large scales or is unable to find a way to import this theory to the smaller scales. That is why we are thinking about Quantum gravity. Science has been searching for a Theory of Quantum gravity for a long time.
In my opinion, such a theory should be based on Planck units. It is best to formulate an idea from the smallest possible situation. In this situation, an object can show its fundamental properties only. If we understand the nature of energy at the Planck level, in any case, it will be the fundamental properties of energy. All the theories we have today, support the idea that gravity is due to the mass of an object. Anyhow, by the equivalency principle, we know that mass is also a form of energy. I would like to say that mass is a feature of energy. We do not consider that a photon has mass, but it does interact with the gravity of other objects. In my opinion, the gravity of an object is not dependent on its mass, it depends on its energy. My theory is based on a geometrical structure of a closed system, and also about how the dimensions are playing in it to change the characteristics of the system. This chapter is an introduction to my ideas about our universe in both microscopic and macroscopic scales. So it can explain the quantum world and visible universe at the same time because I am starting to elaborate my ideas from the very smallest scales. We can observe the fundamental properties of everything in the universe as the same if we go through its possible smallest dimensions. The nature of the particles also changes according to the way energy is distributed.
PLANCK UNITS AND ENERGY
As all, we know that the Planck units are derived from the universal constants c, G, and ħ. here c represents the velocity of light at vacuum, G represents the universal gravitational constant and h represents the Planck constant. The Planck units, which are representing the distance as, Planck length ({\iota }_{\rho }), time as Planck time ({\mathcal{t}}_{\rho }), and mass as the Planck mass ({\mathcal{m}}_{\rho }). These three units are the smallest known fundamental units that we can see in particle physics and quantum mechanics. I wish to start thinking from here. According to these units, we have already calculated the Planck Energy, Volume, Area, and so on. So Planck Energy can be defined as:
{\mathcal{e}}_{\rho }=\sqrt{\frac{\mathfrak{h}{\mathcal{e}}^{5}}{G}}Here I want to describe the micro-universe and the visible universe alike. So by equivalency principle, we can write as:
{\mathcal{e}}_{\rho }={\mathcal{m}}_{\rho }{c}^{2}Here, the speed of light c we can define as (\frac{{\iota }_{\rho }}{{t}{\rho }}{)}. The speed of light does not change even if described in Planck units. So we can rewrite the above equation in a way that we can understand more. Now we can see the three basic dimensions of the universe in this equation.
{\mathcal{e}}_{\rho }={\mathcal{m}}_{\rho }(\frac{{\iota }_{\rho }}{{t}{\rho }}{)}^{2}The left side of this equation represents energy, while the right side explains the nature of that energy. Let’s delve deeper into the right side of the equation to gain a better understanding. We observe that a unit Planck mass is multiplied by the square of the velocity of light. Here, mass refers to the matter it contains, and the square of the speed of light refers to the space-time that matter can affect. So we can say it as: e_{\rho} = \sqrt{\frac{{\mathcal{h}}c^5}{G}} = m_{\rho}\left(\frac{l_{\rho}}{t_{\rho}}\right)^2 = mc^2 . Indeed, the speed of light is a constant; the only factor that can change is mass. But here, all these three dimensions are changing in tandem. Let’s consider a unit of Planck energy as a system. Let’s try to gain a deeper understanding with the help of a picture.
In the figure, the inner sphere represents the amount of matter contained in a system. The outer sphere represents the space-time that the mass inside can influence. Here, matter possesses three dimensions (length, width, and depth), as well as mass. These three dimensions also apply to space-time. There, space and time interact with each other according to the amount of matter contained in that system. At the outermost part of the image, you can see that the amount of space that mass can influence is zero. But there, time is at its highest strength. It is the endpoint of space-time under the influence of matter within that system. Here, time can reach its maximum velocity. It can be observed that the strength of time decreases and the strength of space increases as we approach the matter that is part of the system. This phenomenon is a result of the increasing influence of matter on space. Decrement in the strength of time and increment in the strength of space occur in the same proportion. So, the strength of time and space are equal inside the system. Since the strength of space is highest at the surface of matter within the system, the strength of time becomes zero. So the quantised values (strength) of length (space) and time are equal. So the quantised value of Planck time also equal to \sqrt[3]{m_{\rho}} . If we consider matter alone, we can see that it also has three dimensions, just like space. However, time has no significance in that context. It will contain only matter. Nothing can enter or travel within it. Time is meaningless where it cannot be traversed.
A similar situation occurs in a black hole. Inside a black hole, matter shrinks to its minimum volume. Let’s examine what happens when an atom is absorbed by a black hole. Inside the nucleus of an atom, there is a lot of space between the protons and neutrons. There is even more space available between the nucleus and the electrons. When an atom is absorbed into a black hole, its constituent particles are compressed to their smallest possible state within the black hole. The space inside the atom is absorbed into the space-time of the black hole. Here, a distinction is made between matter and space-time. Here, matter is at its most compressed state. We can represent this situation as: {e}_{\rho }={V}_{\rho }
This is the equation for Planck Energy. When I am looking at this equation, I can realize that this is the smallest amount of energy possible and it is the result of the interaction between the three fundamental Planck units (length, mass, and time). In this equation, we can see the quantized states of Planck units. We can explain this situation through dimensional analysis of a geometric system. I am explaining the geometry below of this theory. So Planck energy is the particular combination of Planck mass, Planck length, and Planck time. I consider this particular state of energy to be a closed system. It is the smallest form of energy, but not the last, so it can add more energy. If we add the “x” quantity of energy to it, the equation will continue as follows.
x{e}_{\rho }=x{m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}I know that all the above equations are familiar in physics, but my understanding or point of view on these equations are allowing me to create strange ideas. Here I am adding the “x” amount of Planck mass on a system, and at the same time have to add the same amount of Planck length and Planck time to the system to fulfill its requirements as energy. We can find that the value of x(\frac{{l}_{\rho }}{{t}_{\rho }}{)} is always constant and represents the speed of light. Now, this system has the ability to grow up by adding more energy to it and can become as a particle or a large size. The only thing we have to notice here is, that the presence of more energy or mass (in Planck scale) in a system, will allow it to accommodate more units of Planck length and Planck time in it. So no matter how much energy a system has, it can be represented on a Planck scale. When we are considering any form of energy as a system we have to consider also the Planck length and Planck time as a source of energy. In this case, I would like to say that these three Planck units represent some source of energy. Also, we know that everything in the universe is under the influence of a universal gravitational constant. So let us write this equation as follows.
Gx{e}_{\rho }=Gx{m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}Now we have the idea of any quantity of energy in the Planck scale. Energy must be permanent in the system with its dimensions. We can never imagine any type of matter in a two-dimensional shape, so I consider that the system will create a three-dimensional shape itself. If a system creates itself a three-dimensional shape, it must have a volume. And here we are coming with the idea of Planck volume to accommodate plank energy because these two are the smallest known units on the same scale. Naturally, we can claim that unit Planck Energy will be perfectly fit in a unit Planck Volume. Mathematically we can represent this situation as:
{e}_{\rho }={V}_{\rho }Here Planck volume is
\sqrt{\frac{(\mathfrak{h}G{)}^{3}}{{c}^{9}}}So
\sqrt{\frac{\mathfrak{h}{\mathcal{e}}^{5}}{G}}=\sqrt{\frac{(\mathfrak{h}G{)}^{3}}{{c}^{9}}}Here both sides of the equation are representing two different things. The left side of the equation represents energy and the right side represents volume. Right now both sides of this equation are dimensionally not matching. Dimensional analysis of this equation tells us, both sides of the equation represent different situations of a system. The dimension of the left side is ({L}^{2}M{T}^{-2}) and the right side is ({L}^{3}). This will never validate an equation. So if we can represent the left side of the equation with respect to “L” (quantized values of Planck mass ({\mathcal{m}}_{\rho }) and Planck time ({\mathcal{t}}_{\rho }), with respect to Planck length ( {\iota }_{\rho }) we can write both sides as volume. The quantized Planck mass with respect to Planck length will represent as ({M}_{\rho }) and accordingly, Planck time will be ({T}_{\rho }). For the Theory Of Everything to be complete, which we are still seeking, unification of dimensions must be possible. In mathematics, we have unified these dimensions. If we take a physical object, mathematically it has three dimensions. We call it length, width, and height. We measure all three dimensions on the same scale. We categorize dimensions in physics as mass, length, and time. All these three are measured on three different scales. We can unify these three dimensions. Here again, I am going to bring the a picture.
In this figure, the space (distance) and the time are equally distributed. If we measure the strength of time and space inside this system, we can see that both are distributed in the same strength. So we can say that time is equal to space (distance). Distribution Of time we can call {T} and distribution of space as {L}.
Now we can bring the equation {e}_{\rho }={V}_{\rho } and its dimensional analysis here. The Planck Energy {\mathcal{e}}_{\rho } is perfectly fit in a planck volume {V}_{\rho}. It will not allow any empty space in it. The dimension of the left side is ({L}^{2}M{T}^{-2}) and the right side is ({L}^{3}). Now we can import the strength of each dimension in this equation. But we still have to find the strength of mass {m}_{s}.
{L}^{2}{M}{T}^{-2}={L}^{3}
Space and time are equal in strength and opposite in direction. The dimensional analysis of the left side of the equation also suggests the same conclusion. So, space and time are canceling strength each other out, leaving mass on the left side of the equation and volume on the right side. So we can say that:
m = VorM = L^3Here, we are simply reduced to two dimensions. But let’s take a closer look at how to achieve this reduction. We can understand this by observing any typical gravitational system. We can interpret this equation in two ways. A given amount of mass will occupy a certain volume. A volume less than this is never possible for that amount of matter. This scope will consist solely of matter. Here, we explain how the three dimensions of matter length, width, and depth (L^3) are distributed. It represents the most stable state of energy. At the time of the formation of the Big Bang singularity, the energy must have been at approximately this state. Then, right from the initial collision, the matter can create a strong gravitational field. Sure, let’s explore another way to explain this equation. The General Theory of Relativity explains the same concept. The dimensions of matter include length, width, and depth, (L^3) along with an additional dimension of space-time (L) that the matter can influence. Here, all three dimensions of matter extend into space-time, so the additional dimension of space-time does not need to be considered.
Now, let’s explore how to relate the strength of mass to this equilibrium between space and time. For that let’s start with the smallest units we know. So, I’m going to insert Planck units into equation the below equation.
m_{\rho} = V_{\rho}orM = L^3orm_{\rho} = l_{\rho}^3If the mass m_{\rho} = l_{\rho}^3, Then the value of length l_{\rho} concerning mρ will be as follows:
l_{\rho} = \sqrt[3]{m_{\rho}}Here, we have linked the length to the mass. So the strength of one unit of Planck length l_{\rho} = 1.616255 \times 10^{- 35}m is equal to \sqrt[3]{m_{\rho}} = \sqrt[3]{2.176434 \times 10^{- 8}}kg. We know that the strength of time and space are equal but in opposite directions. So the value of one unit of Planck time t_{\rho} = 5.391247 \times 10^{- 44}s is equal to \sqrt[3]{m_{\rho}} = \sqrt[3]{2.176434 \times 10^{- 8}}kg. Now, we can rearrange the entire equation using any of these units.
l_{\rho Strength}=t_{\rho Strength}^{- 1}Now we can replace the value of t_{\rho Strength}^{- 1} into the dimensional system.
{m}_{s}={l}_{s}^{3}So this time we can complete the equation as:
l_{\rho Strength}^2l_{\rho Strength}^3l_{\rho Strength}^{- 2} = l_{\rho Strength}^3The left side of this equation clearly declares that it can create a space that is equal to the right side of the equation. Therefore the increasing energy in the system will increase the volume by the same amount. We can state it as follows.
x(\sqrt{\frac{\mathfrak{h}{\mathcal{e}}^{5}}{G}})=x(\sqrt{\frac{(\mathfrak{h}G{)}^{3}}{{c}^{9}}})
Here we consider all these three dimensions as sources of energy. Therefore, the quantized value of these represents the strength of its energy. So the quantized values of these three dimensions are the same always. Now {M}_{\rho } and {T}_{\rho } are having the same dimension of L. In this case, the combination of these three dimensions in a particular mode indicates that the volume of the system or that the system is quantized by energy. We can also avoid all these steps by considering the dimensions as it is, but here I am interested to say that, all these three dimensions are closely related. The picture below will explain more about this concept.
Dimensional configuration. We saw already this picture in the first chapter. But here it is added again as it is needed. This picture shows us, how energy at the Planck scale is obtaining its space in the Unit Planck volume. We can explain this picture in two different ways. The first way we can say that energy is equal to the volume (unit amount of energy can represent in unit volume), which I was explained in the above equation {e}_{\rho }={V}_{\rho }. The next is by considering all these three fundamental dimensions as equal strengths. It is possible when they are quantized and we can experience that in the case of energy. Here Planck length, Planck mass, and Planck time are in a quantized state.
The above equation is representing the relationship between energy and volume and is strictly at the Planck scale. It is very important to describe the gravity of a system. Now we can apply this equation to an atom. But we already know that an atom has its own volume. The problem here is that there is a lot of free space within the atom. So we must have to determine its volume at the Planck scale, to describe its gravity. This volume represents the actual volume of energy, it does not allow any free space inside the system. For example, suppose we fill some air in a balloon. Naturally, that balloon will create a gravitational field. Suppose, we do not release the air in the balloon but make it a little smaller by applying a force on it. It still has no change in its gravitational field because there is no change in the amount of energy inside it. But its surface is closer to its center, so the gravitational force felt on the surface now will be greater than ever. This is an explanation of Newton’s theory of gravity. Let us now consider this in the language of the General Relativity Theory. Gravity In the language of the general theory of relativity is the curvature that energy creates in space-time, where it is located. Let’s see how is it. We already know that energy needs space-time to exist. Let’s see how it curves space-time. Let’s go back to our balloon. Let us assume that it is already located in space-time. Hence its surface is in continuous contact with space-time. If its size suddenly decreases, space-time will be drawn to the balloon’s surface for its survival. An emptiness between the balloon and space-time is not possible. Now you may think that space-time itself is empty. But not so. Space-time is just as important as energy. General relativity theory is describing the relation between space-time and energy. The theory of relativity describes gravity as the curvature of space-time created by energy. Let’s go back to our balloon itself to figure out how. Suppose we refill the balloon without changing its diameter. We know that it is not possible. The balloon expands as we fill the air in it. But let us think like the above. As the air fills up, so does increase the amount of energy inside it, and so does its gravity. This is exactly what Newton and Einstein described. According to the theory of relativity, as gravity increases, it must distort more space-time. As the amount of energy increases it will influence more space-time. This will put more pressure on space-time. Naturally, this pressure is felt most in the area adjacent to the surface of the balloon. This is what we see in black holes. The space-time is so compressed that even light cannot escape. A certain amount of energy will influence a certain amount of space-time. This is what the theory of relativity tells us. Here we can see the change in the free space inside the balloon. Similarly, increasing the diameter of the balloon while retaining the same energy, will change the curvature it creates in space-time. It then absorbs the same space-time into the balloon and reduces the curvature of space-time. Here there is no change in the amount of space-time adjacent to the balloon. Here the gravity of the balloon does not change. The balloon will still have the same influence as it did in the same space-time away from its center. So the size of an atom or a large object plays no role in its gravitational field, and the Planck scale volume determines the gravity of the system in relation to the total energy of the system.
When we are considering this situation ({e}_{\rho }={V}_{\rho }), the quantized Planck mass ({M}_{\rho } ) and Planck time ({T}_{\rho } ) are having the same dimension as the quantized Planck length ({L}_{\rho } ). It is an idea that states the combination of the three basic units (quantized state) will be equal to the Planck volume. So I can say that all these three basic Planck units can also be represented as fundamental dimensions like length, breadth, and height. It is the key idea of this theory. So the energy can be represented in a single unit when all these three basic units are in a quantized state.
Up to now, I was thinking about energy at the Planck scale, now I am intended to think about the fundamental properties of energy at the Planck scale and its reasons. When you think of the smallest units possible, it seems very easy to create ideas. At this stage, we can only have the smallest amount of energy, and space-time which it accommodates. Of course, we cannot ignore the presence of a universal gravitational constant. As a start, let us for a moment forget the existence of a universal gravitational constant. For me, energy is something that is always active. I would like to say that, consciousness is one of the fundamental properties of energy. Energy has a life on its own or it can be a source of life. This is the only reason for the presence of life on our planet. Therefore, the probability of the existence of life occurring, in many other parts of the universe is huge. With this idea, we can explain the evolutionary dynamics of energy in the universe. Now let us try to understand more about the other properties of energy. We find that the energy is in a very limited space (Planck volume) that is self-sustaining there, so things usually end here. But energy is conscious by itself, so things are starting from here.
We can consider the unit Planck energy at the unit Planck volume as a system. When the self-conscious energy tries to confine itself to its confined space-time, the result of the work done by this will spread to outer space-time. This amazing phenomenon we call gravity. This is the same thing that, Sir Isaac Newton called the gravitational force of an object. This is the same phenomenon that according to Albert Einstein’s ideas, extends to space-time and influences the curvature of space-time. This effect allows energy to stay in space-time and allows the curvature of space-time to be created. This is the same thing that leads to the evolution of our universe. So the amount of energy in a system is the reason for gravity. Any amount of energy can create gravity and it is one of the fundamental properties of energy. Mass is just a dimension of energy, like length and time. This is why we claim that a photon has no mass but can interact with gravity. This idea can resolve the puzzles of dark matter and dark energy. For this reason, I am considering energy as a combination of three basic dimensions (we can unify these three units with the three fundamental dimensions like length, breadth, and height) like Planck length, Planck time, and Planck mass. We can define gravity in a simple way, as the result of the work done by unit energy in unit volume at the Planck scale.
{m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}({V}_{\rho })={S}_{\rho }This equation states that the product of energy and volume at the Planck scale is creating the Planck space-time “sρ“. This equation is giving us the idea of Planck space-time concerning the Planck energy, but I am looking for an equation that relates the space-time with the dimensions of volume. So volume is calculated as a form of energy as I described in the above equations. This equation can be represented as follows:
({V}_{\rho })({V}_{\rho })=({V}_{\rho })^{2} {S}_{\rho }=({V}_{\rho })^{2}These equations represent the space-time that a unit of Planck energy can create. We can also say that ({V}_{\rho })^{2} is the amount of space-time in which a unit of Planck energy can create a curvature. So from here, we can see that the gravity of unit energy can only affect a fixed space-time. It can create a curvature on space-time at a limited volume. Hence I can say that gravity of any amount of energy has a limited range, and I cannot say that gravity can make effects in an infinite range. Of course, everything in the universe is under the influence of universal gravity, that’s why we are allowing universal gravitational constant G in our equations for gravity. It doesn’t mean that gravity of a system has an infinite range. I can never believe that a steel ball of one kilogram has an infinite range of gravity.
G{S}_{\rho }=G({V}_{\rho })^{2}To explain more about gravity and other properties of energy, the dimensions of the system need to be discussed. We know that particles are showing different properties like different spin, different charges, and all. To realize the reason for these properties, we must have to know more about the dimensions. Dimensional variations can determine the basic properties of a particle. Dimensional variations can determine the basic properties of a particle. It is a simple idea, but if we elaborate on it, this idea is applicable in a wide range. We are living in a three-dimensional universe, but the General Theory of Relativity is suggesting space-time as the fourth dimension. Many other theories argue that the universe has even more dimensions. I am considering it as a spatial dimension, that occurs when matter projects its effects on space-time. The universe is actually a state in which three-dimensional matter is located in space-time. I like to believe that we live in such a three-dimensional universe. Matter is located in space-time. So we are keeping space-time as the fourth dimension. In this part, I am discussing the three dimensions of a closed system, where the unit Planck energy is accommodated. So, I am interested to work with three dimensions because matter can only have three dimensions. It can neither shrink to a two-dimension nor achieve the fourth dimension. Three dimensions are a basic property of matter (energy). We may discuss more the spatial dimensions later when we are trying to understand more about gravity. It is not necessary to discuss more spatial dimensions, because we already have a successful theory of gravity by Albert Einstein, which explains the dimensions of space-time.
Here I am about to describe, how these three dimensions (length, breadth, and height) are playing a crucial role to determine the basic properties of matter (we can insert the quantized length, mass, and time at the Planck scale into these three dimensions). To explain my ideas I am starting with a two-dimensional shape. My idea is to get a life with a simple thought experiment. It is familiar in mathematics and I am going to elaborate this idea into the dimensional properties of matter when we can consider it as a system. And we know that we have mass, length, and time in the system. Let us try to unify these three fundamental units with the three fundamental dimensions. I can explain it with the help of a picture, I think it will be more helpful to understand the idea perfectly. This is the best idea to describe the nature of gravity in different situations. We can analyze how gravity gets changes according to the changes in the dimensions inside the system. Also, this idea is the only helpful clue to describe the nature of a system.
Picture: Dimensional variations of a system
Imagine that I have a square with a fixed length and area. This is a two-dimensional shape, and we can make changes on one of its dimensions, by keeping the area the same, as shown in the picture. Here we have the length and breadth as the two dimensions. This figure shows the different situations that occur when this square has differences in its dimensions. At the initial stage, it was a perfect square. Then gradually it changes one of its dimensions and it becomes a rectangle. And it continues this process and the dimension is forced to undergo a reverse process, to become a square again. After reaching a certain point, it is unable to keep its volume the same, so it is forced to change its characters and becomes a square in the opposite direction. This picture is just an example, it can change its dimensions from left to right or upward to downward and vice versa. So here the actual nature of the shape is varying while the rate of change in dimension keeps the same direction. Here I am replacing these two dimensions into the basic units of length and time, with the help of the above-mentioned statements of this chapter. Now, this two-dimensional shape becomes the measurements of time and length. So while calculating velocity, according to the path of its dimensional part of the length, we can create an arbitrary two-dimensional shape. This situation is important to explain the nature of energy in phases with different dimensions. The same idea is applicable in three-dimensional shapes, so we can apply this to the volume of a three-dimensional shape.
We can observe the same process by importing this idea into a three-dimensional shape. We are applying the same methods here, so it is not necessary to explain more about the applications of this idea in a three-dimensional shape. By changing any of its dimensions, we can change the characteristics of the shape. What we are interested in three-dimensional shape is that matter can be accommodated in a three-dimensional space only. The only thing we need to look at is to keep the volume the same. If we consider it as a system, we can analyze the changes happening to the system. Now we can import the concept of mass, time, and length into this system. It would be easier if we imagine these units on the Planck scale. By changing these units (dimensions) in this system upon the same volume, we can experience the changes in its basic characters. By accepting time, length, and mass as a source of energy, the total system will experience different natures, upon changes in any of these sources. If we make changes to any one dimension, it will affect the volume of the system. In this way, we cannot keep the volume of the system the same. Always we must have to make changes to any two of these three dimensions. The mass is not changeable. So we can only adjust the space and time. So we can call it a dimensional adjustment. This idea will change our present concepts about energy and the universe itself. I would like to use the same idea to explain gravity. The below picture will give us more explanations.
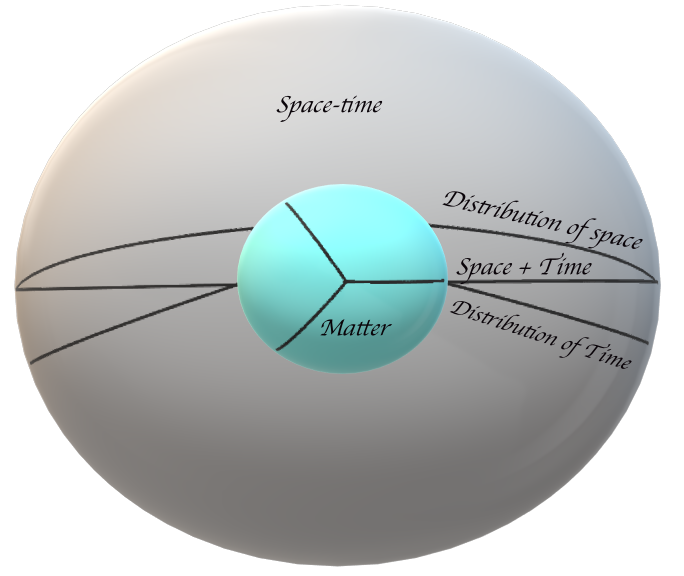
Picture: gravitational system
This picture explains my ideas about gravity. The inner circle in this picture ({e}_{\rho }={V}_{\rho }) represents the unit of Planck energy and at the Planck volume. So this is the smallest possible space in which energy can get accommodated. The lines inside the inner circle ({M}_{\rho }) and ({L}_{\rho }) represents the Quantized Planck mass and Planck length accordingly. The line CD ({T}_{\rho }) represents the quantized Planck time and I have placed it at this position in this picture, to get a more convincing understanding of the dimensional changes. The outermost circle G{S}_{\rho }=G({V}_{\rho })^{2}, represents the total curved space-time by unit energy, or the volume of the curved space-time. The point O represents the dimensional change position. The arbitrary triangle BAC represents the distribution of space and the arbitrary triangle DCA represents the distribution of time accordingly. Here we can see the distribution of time and space are in opposite directions. Line AC is the radius of the total gravitational field of the system.
I am going to explain how gravity is created by a unit volume of energy and how the dimensional changes will affect its fields. It is not necessary to explain the curvature of space-time here, we just need to check, how this theory interacts with the General Theory of Relativity. Gravity is the influence exerted on space-time as a result of the work done by a unit of Planck energy per unit plank volume. It can make a curvature on a fixed volume of space-time in accordance with its dimensional shape. If I repeat it with respect to Newtonian gravity, I can say that it will create a fixed force (field) in the space to interact with other forms of energy. In this picture, we can see that the gravitational field is divided into two sections at a point O. This is an imaginary point where the gravitational fields get reversed. To get a better idea, I wish to divide this into two parts like x and y.
x({m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}({V}_{\rho }))G+y({m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}({V}_{\rho }))G=G{S}_{\rho } x(({V}_{\rho })({V}_{\rho }))G+y(({V}_{\rho })({V}_{\rho }))G=G({V}_{\rho })^{2} x({m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}({V}_{\rho }))G+y({m}_{\rho }(\frac{{l}_{\rho }}{{t}_{\rho }}{)}^{2}({V}_{\rho }))G=x(({V}_{\rho })({V}_{\rho }))G+y(({V}_{\rho })({V}_{\rho }))GThe first part represents the Space-dependent field and the second part represents the time-dependent field. So imagine that the first section contains a field with x distance of its radius, and the second section contains a field with y distance of its radius. These two values of x and y can create its own volume in the curved space-time and the sum of these two volumes will be the actual curved space-time. Here we can imagine, that Space and time are distributed uniformly at each distance of this field. The picture shows us that they are distributing with opposite directions. It is already proved by Sir Isaac Newton and Albert Einstein in the theories of gravity. So we can see that the strength of the spatial field is decreasing from the center of the system and it will be zero at the end of the curved space-time. Same like, the strength of the time field will decrease from the starting point of the curved space-time and it will be zero at the center of the system. Increasing the volume of the field will decrease the strength of gravity. So the distribution of the spatial field, near the center will be high because the volume of the field here is very small. This is the general idea of a gravitational field and the gravitational strength of a system. I have not mentioned any tensor fields in this equation because here I am describing the strength of the gravitational field of an individual system. When we consider the influence of an external field, we must have to apply different variations depending upon the influencing fields. Now we will look, how the dimensional dance will affect the strength of the gravitational fields at each level. I can clearly state that the configuration of dimensions in a system will directly affect the strength of the gravitational field of the system. The volume of the gravitational field or the curved space-time must be always the same always, even if it changes its dimensional configurations. I have been explained above, that the system is a combination of three dimensions. So if it makes any changes in any two dimensions, it will affect the strength of the field. As per the picture, if we increase the dimensional values of the Space, the system must have to reduce the dimensional values of the time. This situation will increase the strength of the spatial field inside the curved space-time, which will tend to reduce the strength of the time field. So, by changing the configuration of dimensions, a mass can show different strengths of gravitational fields. If the earth has another dimensional configuration, we will experience a different gravitational strength.
Here I am introducing a new idea to determine the strength of the gravitational field at different stages. It states that gravity has a finite range. What we are experiencing in the earth’s gravity is one of its possible dimensional configuration states. The dimensional configuration of a system can determine the basic nature of the system. In physics, we are studying a lot of particles. We also discuss the possibilities of many particles that we do not yet know. We know that they are all made of energy. But each of them has different characteristics. The main reason for all this is the dimensional configurations of those particles. This dimensional configuration can explain the evolution of the universe by accepting that energy is self-conscious. By accepting that energy itself can be a form of life, we can state that the universe was created by itself. The probability of the existence of life in any part of the universe is very high.
This theory can generate very valuable information related to dark energy and dark matter. In the next chapter, I am trying to describe how gravity is working in curved space-time. Or how it is interacting with the curved space-time of another system. Those things are well explained in the Theory of General Relativity already. I want to know more about it from my point of view.

